Brojački i koncentrični ciklusi - Zadaci

Brojački ciklusi se mogu posmatrati kao specijalna vrsta ciklusa sa preduslovom Kod ovih ciklusa postoji promenljiva (brojač) koja dobija različite vrednosti koje su u rasponu od početne pa do krajnje. Za svaku vrednost promenljive izvršava se po jedna iteracija ciklusa. Za razliku od uslovnih ciklusa, koji se izvršavaju dok je neki uslov zadovoljen, ovde se na početku ciklusa tačno zna koliko će se puta izvršiti.

Zadaci za vežbu

Zadatak 1
Unosi se pozitivan celi broj N.
a) Ispisati sve cele brojeve od 2 do 2N.
b) Ispisati sve cele brojeve od N do 1.

Zadatak 2
Unosi se pozitivan celi broj N.
a) Izračunati N! (faktorijel od N - računa se kao 1*2*3*4*...*N).
b) Izračunati 2^N.

Zadatak 3
Za uneto celobrojno, pozitivno N izračunati sledeće sume:

a) 

b) 

Zadatak 4
Za unete brojeve a (različito od 0) i N (ceo broj) izračunati sledeću sumu:

Zadatak 5
Za unete cele, pozitivne brojeve X i N izračunati sumu:

Zadatak 6
Za unete cele, pozitivne brojeve X i N izračunati sume:

a) 

b) 

c) 

Zadatak 7
Za unete brojeve X i N (gde je X > N) izračunati proizvod:

Zadatak 8
Napravite algoritam koji na osnovu unetog broja meseca M i dana u mesecu D (podrazumevamo da je to neka godina koja nije prestupna), određuje redni broj tog dana u godini (od 1 do 365).

Cikluse možemo smestiti i jedan unutar drugog. Na taj način postižemo da se za svaku iteraciju spoljnog ciklusa u celosti izvrši unutrašnji ciklus.

Ugnježdeni ciklusi su tehnika programiranja, a ne vrsta ciklusa. Možemo ih kreirati sa brojačkim, ali i uslovnim ciklusima.

Vodite računa - koncentrični ciklusi su poznati kao "smrt" za brzinu izvršavanja programa pošto se broj iteracija višestruko povećava. Naravno, postoji puno situacija kod kojih se ne mogu izbeći, samo kažemo da ih ne koristite olako.

Zadaci za vežbu

Zadatak 1
Ispisati tablicu množenja svih brojeva od 1 do 10.
a) Svi rezultati se prosto ispisuju jedan ispod drugog.
b) Rezultati su su ispisani jedan ispod drugog, ali tako da se ne ponavljaju ista množenja (npr. ako smo već ispisali rezultat za 2*3, ne ispisujemo za 3*2).
c) Rezultati treba da budu ispisani u tablici 10x10.

Zadatak 2
U RPG igri se bore ratnik i ork. Snaga i veština su im izjednačene, pa se ishod borbe određuje bacanjem jedne osmostrane (brojevi od 1 do 8) kocke za orka i obične šestostrane (1 do 6) kocke za ratnika. Oba igrača će preživeti samo u slučaju da je razlika dobijenih brojeva manja od 3. Ispisati kolika je verovatnoća da se to desi.

Zadatak 3
Minsko polje se sastoji od NxM polja. Bomba se nalazi na onim poljima čiji proizvod reda i kolone umanjen za jedan daje paran broj. Ispisati broj polja na kojima nema bombe.

Zadatak 4
Ispisati svaki trocifreni broj za koji važi da je deljiv brojem koji se dobija izbacivanjem njegove srednje cifre. Npr. jedan od takvih brojeva je 143 zato što je 143 deljivo sa 13 (13 se dobija izbacivanjem srednje cifre iz 143).

Zadatak 5
Sef se otvara kombinovanjem tri brojčanika. Na prvom se nalaze brojevi od 1 do 12, na drugom su parni brojevi od 0 do 10, a na trećem su brojevi 3, 5 i 7. Sef se otvara samo kombinacijom čiji je zbir jednak unetom broju X (u rangu od 4 do 29). Ispisati sve kombinacije koje otvaraju sef.

Zadatak 6
Napraviti algoritam kojim se ispisuju svi savršeni brojevi u intervalu od 2 do X (X se unosi kao ceo broj, veći od 1). Broj je savršen ako je jednak sumi svojih delitelja (uključujući 1, a isključujući njega samog).
Npr. broj 28 je savršen jer je 28 = 1+2+4+7+14.

Zadatak 7
Digitalni časovnik prikazuje vreme u satima, minutima i sekundama. Ispisati svaki trenutak u toku jednog dana kada je zbir cifara na časovniku jednak unetom broju N.
Npr. za uneto N=6, prikazati rezultat na sledeći način:

Zadatak 8
Ako se unese novčani iznos N, potrebno je ispisati sve mogućnosti da se taj iznos isplati korišćenjem M novčića ako imamo samo novčiće od 1, 3 i 5 dinara.
Npr. ako iznos N=41 želimo da isplatimo sa M=9 novčića, to možemo učiniti na dva načina: 2 novčića od 3 i 7 novćića od 5 dinara ili 1 novčić od 1 i 8 novćića od 5 dinara.

Zadatak 9
Imamo neispravan digitalni časovnik koji svakog minuta povećava broj minuta za M i broj sati za S. Vrednosti S i M se unose i podrazumeva se da je S u rangu od 0 do 23, dok je M u rangu od 0 do 59. Pri tom, kada minuti prevaziđu vrednost 59, sati se ne povećavaju dodatno za jedan. Napravite algoritam kojim se proverava koliko puta u toku dana ovaj sat pokaže tačno vreme, ako ga namestimo da u ponoć počne od 00:00.
Dakle, ako se unesu S=3 i M=25, časovnik će raditi na sledeći način:

Ovde imamo i nekoliko grafičkih zadataka koji koriste brojačke ili ugnježdene cikluse.

Zadaci za vežbu

Zadatak 1
Za unet broj polja n (pozitivan ceo broj, veličine npr. od 10 do 50), iscrtati mrežu linija koje kreiraju zadat broj polja po horizontali i vertikali.

Zadatak 2
Za unet poluprečnik R (pozitivan ceo broj, veličine od 10 do 100), izvršiti animaciju kretanja kruga poluprečnika R sa leve na desnu stranu grafičkog prozora, s tim da se uvek vidi ceo krug.

Zadatak 3
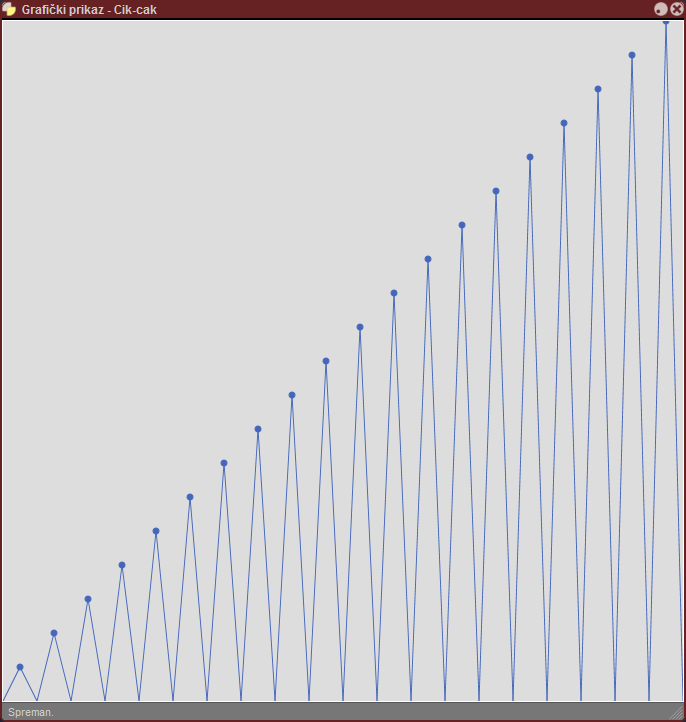
Unosi se celi broj N, od 1 do 50. Nacrtati cik-cak liniju od 2N+1 temena, kao na priloženoj slici. Linija ide kroz celu širinu grafičkog prozora. Svako neparno teme treba da bude vezano za donju ivicu prozora, a svako parno teme se izdiže sve više dok ne stigne do vrha prozora. U prevodu - treba nacrtati N "šiljaka", gde je svaki veći od prethodnog, tako da je uvećanje ravnomerno sve do pune visine grafičkog prozora. U svakom vrhu "šiljka", odnosno parnog temena, nacrtati krug poluprečnika 3 piksela.

Zadatak 4
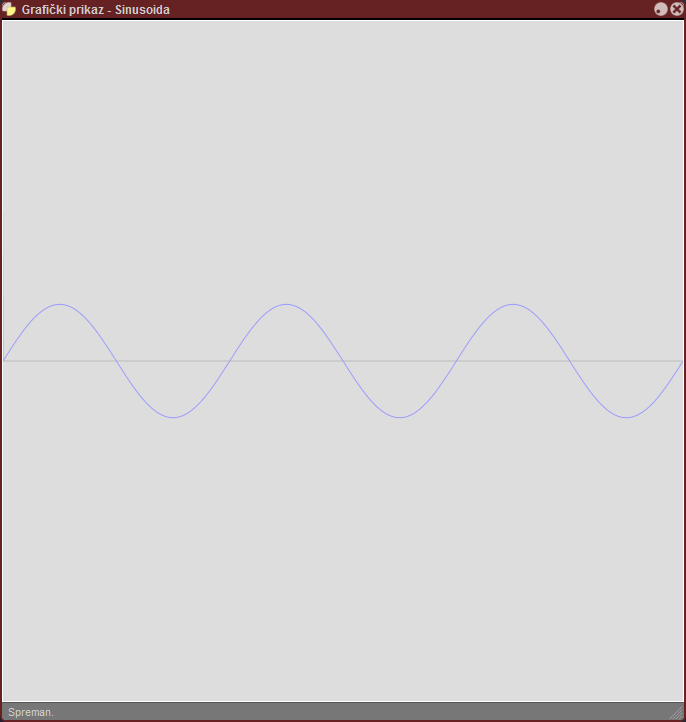
Nacrtati sinusnu funkciju koja se sastoji od N punih sinusoida (2PI). Nacrtati i X osu na sredini grafičkog okvira.

Zadatak 5
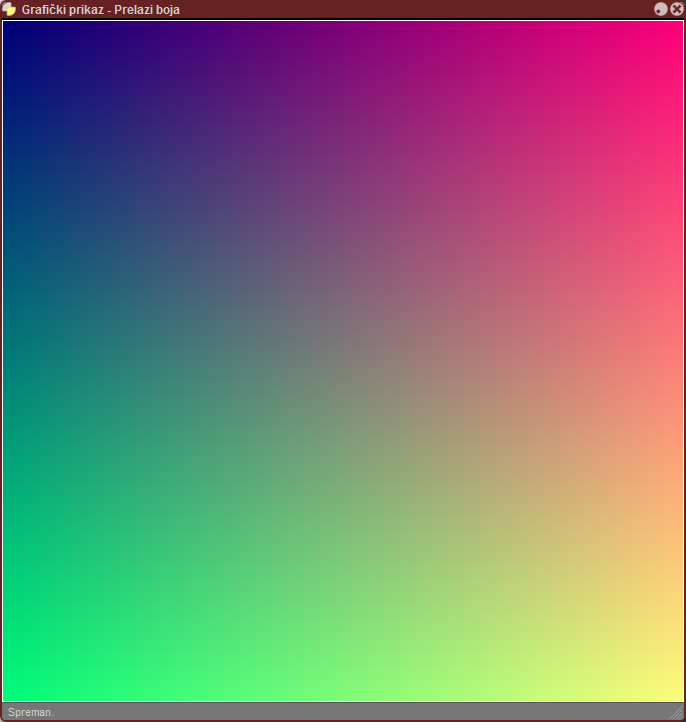
Popuniti grafički okvir sa 100x100 obojenih pravougaonika, ali tako da svaki bude obojen drugačijom bojom. Boje formirati kolornom funkcijom rgba(), tako da se crvena komponenta menja od minimuma do maksimuma po horizontali, a zelena komponenta isto tako po vertikali. Plava komponenta uvek iznosi 120.

Zadatak 6
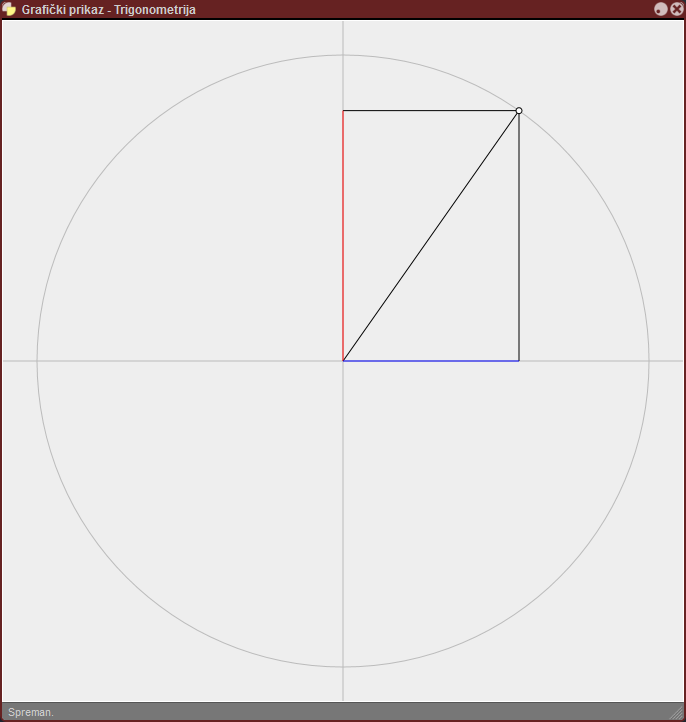
Napraviti animaciju kružića koji se kreće po velikoj kružnici. Ova animacija treba da ilustruje trigonometrijske funkcije sin() i cos(). Znači da treba da prikažemo i sve pomoćne linije, kao i da posebno označimo vrednost sinusa na y-osi i kosinusa na x-osi. Neka animacija bude beskonačna.

Zadatak 7
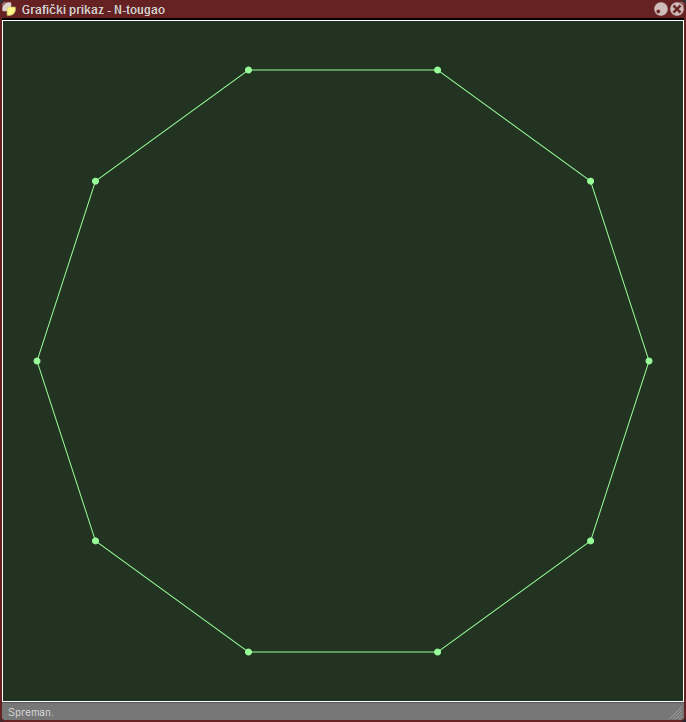
Unosi se broj temena N, kao celi broj od 3 do 50
a) nacrtati pravilan N-tougao
b) nacrtati pravilan N-tougao, kod koga je svako teme povezano sa svima ostalima

N-tougao treba da se nalazi u centru grafičkog prozora. Veličina treba da mu bude 90% visine grafičkog prozora. Svako teme N-tougla ćemo istaknuti tako što ćemo nacrtati krug poluprečnika 3 piksela.